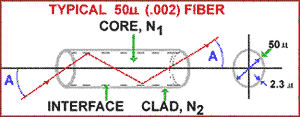
The figure above depicts a section of a clad cylindrical fiber showing the core with refractive index of N1 and the clad with index of N2. Also shown is a light ray entering the end of the fiber at angle (A), reflecting from the interface down the fiber. However, if angle A becomes too great, the light will not reflect at the interface, but will leak out the side of the fiber and be lost. This angle, beyond which light cannot be carried in a fiber, is called the CRITICAL ANGLE and may be calculated from the two indices of refraction.
To calculate the Critical Angle, first determine the N.A. (Numerical Aperture).The N.A. of any glass combination may be calculated as follows: (where N1= the index of refraction of the core glass), and N2=(the index of refraction of the cladding glass):
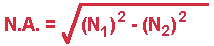
For example, taking 1.62 for N1 and 1.52 for N2 , we find the NA to be .56. By calculating the arc sine (sin-1) of .56 ( 34 degrees) we determine THE CRITICAL ANGLE.
As this fiber accepts light up to 34 degrees off axis in any direction, we define the ACCEPTANCE ANGLE of the fiber as twice the critical angle or in this case, 68 degrees.
Try our acceptance angle calculators below:
For your further information, the F/ NUMBER EQUIVALENT of the N.A. is calculated as follows:

The Numerical Aperture is an important parameter of any optical fiber, but one which is frequently misunderstood and overemphasized. In the first illustration above, notice that angle A is shown at both the entrance and exit ends of the fiber. This is because the fiber tends to preserve the angle of incidence during propagation of the light, causing it to exit the fiber at the same angle it entered. Now look at the figure below, which is a drawing of a typical light guide being illuminated by a projector type lamp.
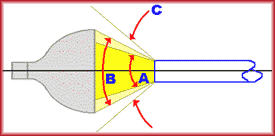
Angle A (29 degrees) is the acceptance angle of a N.A. .25 fiber. Angle B (45 degrees) is the incident angle from the bulb. Angle C (83 degrees) is the acceptance angle of a N.A. .66 fiber.
Calculating the N.A. for the 45 degree angle (B) of incidence yields .38 (sin(45/2)). Therefore, fiber with an N.A. of .66 will accept all of the light from the bulb, but the output cone at the other end will be 45 degrees, not the 83 degrees that you might expect. Conversely, the N.A. .25 fiber is not capable of accepting all the light from the bulb. Any light transmitted through this fiber will create an output cone of 29 degrees.
Many people believe that using a low N.A. fiber will “focus” the light from a wider N.A. source. This is not true. As you see, the lower N.A. fiber simply has a lower acceptance angle. While the resulting output will be projected into a tighter area, the overall light transmitted is less than what might be transmitted through a higher N.A. fiber. To focus light from a source, a lens assembly must be used to gather all available light and change the incident angle (and resulting N.A.) to match, (or be less than) the N.A. of the fiber being used.
Additionally, (and somewhat confusing) although the law of physics state the angle of incidence must equal the angle of reflection, life will get in the way when light tavels through longer fibers and fiber bundles. Impurities in glass alter the propagation angle over length such that, if the fiber or fiber bundle is long enough, regardless of input angle, the emitting angle will equal the acceptance angle of the fiber in step index fibers.
If you know the input launch angle of the light beam, you can determine the size of the spot when it’s projected from the end of a Fiber optic fiber or component (at any distance) by using some simple trigonometry. If you’re using a collimator, you can also determine the spot size (and the change in the output angle). We’ve made it simple for you! Use our Excel Numerical aperture calculator.
Many people believe that using a low N.A. fiber will “focus” the light from a source. This is not true. A narrow N.A. fiber simply admits less light than a wider N.A. fiber, assuming the source is emitting light at a wide N.A..

